
노이즈의 근본인, 파동(wave)과 파동의 성질을 살펴보자.
파동의 두 가지 중요한 특성은 진폭과 주파수이다.
간단한 선형(1차원) 파동의 방정식은 다음과 같다.
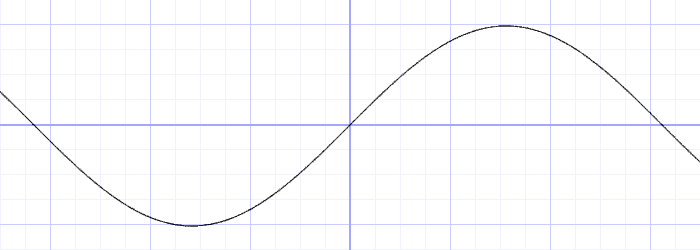
float amplitude = 1.;
float frequency = 1.;
y = amplitude * sin(x * frequency);
파동의 또 다른 특성은 합산할 수 있다는 것이다. ( 두 개 이상의 파동을 합침)
이는 공식적으로 superposition(중첩)이라고 불린다.

// 위 이미지 참고링크
https://www.acs.psu.edu/drussell/demos/superposition/superposition.html
// 예제
진폭과 주파수가 다른 파동을 더하면 모양이 어떻게 되는지 주목하라.

float amplitude = 1.;
float frequency = 1.;
y = sin(x * frequency);
float t = 0.01*(-u_time*130.0);
y += sin(x*frequency*2.1 + t)*4.5;
y += sin(x*frequency*1.72 + t*1.121)*4.0;
y += sin(x*frequency*2.221 + t*0.437)*5.0;
y += sin(x*frequency*3.112+ t*4.269)*2.5;
y *= amplitude*0.06;
이제 사인파 대신 펄린 노이즈를 사용해보자.
펄린 노이즈는 기본적인 형태는 사인파와 비슷한 모양과 느낌을 가지고 있다.
진폭과 주파수를 보면 조금의 차이를 느낄 수 있다.
진폭은 상당히 일정한 편이다.
주파수는 중심 주파수를 중심으로 상당히 좁다.
하지만 사인파만큼 규칙적이지는 않다.
여러 스케일을 갖도록 노이즈를 만들고, 합산하여 랜덤하게 보이도록 하는 것이 더 쉽다.
사인파의 합을 랜덤하게 보이게 하는 것도 가능하긴 하다.
하지만 주기적이고 규칙적인 특성을 숨기려면 다양한 파형이 필요하다.
규칙적인 단계로 주파수(frequency)를 연속적으로 증가시킨다.
또한 노이즈의 진폭(게인)을 감소시키는 다양한 노이즈 반복(옥타브)을 추가한다.
이러면, 노이즈가 더 디테일해진다.
이 기법을 "프랙탈 브라운 운동"(fBM) 또는 간단히 "프랙탈 노이즈"라고 한다. (fractal brown motion)
가장 간단한 형태의 예제를 보자.
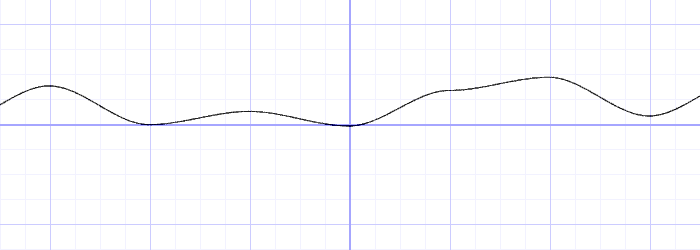
// Properties
const int octaves = 1;
float lacunarity = 2.0;
float gain = 0.5;
//
// Initial values
float amplitude = 0.5;
float frequency = 1.;
//
// Loop of octaves
for (int i = 0; i < octaves; i++) {
y += amplitude * noise(frequency*x);
frequency *= lacunarity;
amplitude *= gain;
}옥타브가 추가될 때마다 곡선이 더 세밀해진다.
또한 유사한 형태로 옥타브가 추가되는 것에 주목하라.
곡선을 확대해보자.
일부분은 전체와 비슷한 패턴을 갖는다.
이는 수학적 프랙탈의 중요한 특성이다.
예제에서는 반복문을 통해 이 특성을 시뮬레이션 하고 있는 것이다.
반복을 몇번하여 합을 구한 후, 반복을 중단하기 때문에, 실제 프랙탈을 생성하는 것은 아니다.
하지만 이론적으로 영원히 반복하고 노이즈 성분을 무한히 추가하면 진정한 수학적 프랙탈을 얻을 수 있다.
컴퓨터 그래픽에서는 물체가 픽셀보다 작아지는 경우처럼 표현할 수 있는 범위에 한계가 있다.
그래서 프랙탈 모양을 만들기 위해 무한대의 합을 만들 필요는 없다.
다음 코드는 프랙탈처럼 보이는 패턴을 만들기 위해 fBm을 2차원으로 구현하는 예시이다.

float random (in vec2 st) {
return fract(sin(dot(st.xy,
vec2(12.9898,78.233)))*
43758.5453123);
}
// Based on Morgan McGuire @morgan3d
// https://www.shadertoy.com/view/4dS3Wd
float noise (in vec2 st) {
vec2 i = floor(st);
vec2 f = fract(st);
// Four corners in 2D of a tile
float a = random(i);
float b = random(i + vec2(1.0, 0.0));
float c = random(i + vec2(0.0, 1.0));
float d = random(i + vec2(1.0, 1.0));
vec2 u = f * f * (3.0 - 2.0 * f);
return mix(a, b, u.x) +
(c - a)* u.y * (1.0 - u.x) +
(d - b) * u.x * u.y;
}
#define OCTAVES 6
float fbm (in vec2 st) {
// Initial values
float value = 0.0;
float amplitude = .5;
float frequency = 0.;
//
// Loop of octaves
for (int i = 0; i < OCTAVES; i++) {
value += amplitude * noise(st);
st *= 2.;
amplitude *= .5;
}
return value;
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(0.0);
color += fbm(st*3.0);
gl_FragColor = vec4(color,1.0);
}
이 기법은 절차적 랜드스케이프를 만드는데 사용되기도 한다.
산을 만드는 침식(erosion) 프로세스는 아주 큰 스케일에서 이러한 자기 유사성을 생성하는 방식으로 작동한다.
그래서 fBm은 산을 만드는데 적합하다.
이 용도에 관심이 있다면, 이니고 퀼레스의 advanced noise에 관한 글을 읽어보라.

// valley
이러한 기법을 응용하여, 터뷸런스와 같은 효과를 얻을 수도 있다.
이는 본질적으로 fBm이지만 signed noise를 절대값으로 만들어, 급격한 계곡(valley)을 만든다.

for (int i = 0; i < OCTAVES; i++) {
value += amplitude * abs(snoise(st));
st *= 2.;
amplitude *= .5;
}
// ridge
이 알고리즘의 또 다른 응용으로는 급경사 계곡을 거꾸로 뒤집어 날카로운 꼭대기(ridge)를 만드는 것이다.

n = abs(n); // create creases
n = offset - n; // invert so creases are at top
n = n * n; // sharpen creases
또 다른 응용은 노이즈를 더하는 대신 곱하는 것이다.
루프의 이전 조건에 따라, 후속 노이즈 함수의 scale을 조정하는 것도 흥미롭다.
이렇게 하면 프랙탈의 엄격한 정의에서 벗어나, 상대적으로 덜 알려진 '다중 프랙탈'이라는 기술을 사용한 것이다.
다중 프랙탈은 수학적으로 정의되지는 않았지만, 그래픽 분야에서 유용하다.
실제로 멀티프랙탈 시뮬레이션은 지형 생성을 위한 최신 상용 소프트웨어에서 매우 보편적으로 사용된다.
자세한 내용은 Kenton Musgrave의 책인, Texturing and Modeling: a Procedural Approach" (3rd edition)
16장을 읽어보기 바란다.
안타깝게도 이 책은 몇 년 전에 절판되었다.
초판의 PDF 버전은 온라인에서 구매할 수 있다.
하지만 3판의 지형 모델링 기능이 전혀 포함되어 있지 않아서 추천하지 않는다.
Domain Warping
이니고 퀼레스는 fBm의 좌표를 왜곡하는 방법에 대해서도 흥미로운 글을 썼다.

https://iquilezles.org/articles/warp/
이 기법의 덜 극단적인 예는 다음 코드에서 wrap을 사용하여 구름과 같은 텍스처를 생성하는 것이다.
결과물에 자기 유사성이 어떻게 표현됐는지에 주목하라.

float random (in vec2 _st) {
return fract(sin(dot(_st.xy,
vec2(12.9898,78.233)))*
43758.5453123);
}
// Based on Morgan McGuire @morgan3d
// https://www.shadertoy.com/view/4dS3Wd
float noise (in vec2 _st) {
vec2 i = floor(_st);
vec2 f = fract(_st);
// Four corners in 2D of a tile
float a = random(i);
float b = random(i + vec2(1.0, 0.0));
float c = random(i + vec2(0.0, 1.0));
float d = random(i + vec2(1.0, 1.0));
vec2 u = f * f * (3.0 - 2.0 * f);
return mix(a, b, u.x) +
(c - a)* u.y * (1.0 - u.x) +
(d - b) * u.x * u.y;
}
#define NUM_OCTAVES 5
float fbm ( in vec2 _st) {
float v = 0.0;
float a = 0.5;
vec2 shift = vec2(100.0);
// Rotate to reduce axial bias
mat2 rot = mat2(cos(0.5), sin(0.5),
-sin(0.5), cos(0.50));
for (int i = 0; i < NUM_OCTAVES; ++i) {
v += a * noise(_st);
_st = rot * _st * 2.0 + shift;
a *= 0.5;
}
return v;
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy*3.;
// st += st * abs(sin(u_time*0.1)*3.0);
vec3 color = vec3(0.0);
vec2 q = vec2(0.);
q.x = fbm( st + 0.00*u_time);
q.y = fbm( st + vec2(1.0));
vec2 r = vec2(0.);
r.x = fbm( st + 1.0*q + vec2(1.7,9.2)+ 0.15*u_time );
r.y = fbm( st + 1.0*q + vec2(8.3,2.8)+ 0.126*u_time);
float f = fbm(st+r);
color = mix(vec3(0.101961,0.619608,0.666667),
vec3(0.666667,0.666667,0.498039),
clamp((f*f)*4.0,0.0,1.0));
color = mix(color,
vec3(0,0,0.164706),
clamp(length(q),0.0,1.0));
color = mix(color,
vec3(0.666667,1,1),
clamp(length(r.x),0.0,1.0));
gl_FragColor = vec4((f*f*f+.6*f*f+.5*f)*color,1.);
}이러한 방식으로 노이즈로 텍스처 좌표를 왜곡하는 것은 매우 유용하고 재미있다.
하지만 마스터하기는 매우 어렵다.
강력한 도구이지만 잘 사용하려면 많은 경험이 필요하다.
이렇게 왜곡하는데 유용한 방법은 노이즈의 미분(그래디언트 또는 기울기)으로 좌표를 이동시키는 것이다.
Ken Perlin과 Fabrice Neyret의 유명한 논문인 "flow noise"는 이 아이디어를 기반으로 한다.
펄린 노이즈의 최신 구현 방식에는 그래디언트도 같이 계산하는 방식을 사용한다.
위와 같이 "실제" 그래디언트를 사용할 수 없는 경우, 근사치를 구해 사용해야한다.
하지만 정확도가 낮고 더 많은 작업이 필요하다.
'셰이더 (Shader) > The Book of Shaders (완)' 카테고리의 다른 글
| [GLSL] 12 - Cellular Noise (0) | 2023.05.03 |
|---|---|
| [GLSL] 11 - Noise (0) | 2023.04.26 |
| [GLSL] 10 - Random (0) | 2023.04.25 |
| [GLSL] 9 - Patterns (0) | 2023.04.20 |
| [GLSL] 8 - 2D Matrices (1) | 2023.04.20 |




댓글