
Translate
도형을 이동하는 방법은 좌표계 자체를 이동하는 것이다.
st 변수에 각 도형의 위치 벡터를 더한다.
이러면 전체 공간 좌표계가 움직인다.

코드 예제를 보자.

float box(in vec2 _st, in vec2 _size){
_size = vec2(0.5) - _size*0.5;
vec2 uv = smoothstep(_size,
_size+vec2(0.001),
_st);
uv *= smoothstep(_size,
_size+vec2(0.001),
vec2(1.0)-_st);
return uv.x*uv.y;
}
float cross(in vec2 _st, float _size){
return box(_st, vec2(_size,_size/4.)) +
box(_st, vec2(_size/4.,_size));
}
void main(){
vec2 st = gl_FragCoord.xy/u_resolution.xy;
vec3 color = vec3(0.0);
// To move the cross we move the space
vec2 translate = vec2(cos(u_time),sin(u_time));
st += translate*0.35;
// Show the coordinates of the space on the background
// color = vec3(st.x,st.y,0.0);
// Add the shape on the foreground
color += vec3(cross(st,0.25));
gl_FragColor = vec4(color,1.0);
}Rotations
객체를 회전하려면 행렬을 사용한다.
행렬은 열과 행으로 구성된 숫자의 집합이다.
벡터의 값을 수정하기 위해 규칙에 따라 벡터에 행렬을 곱한다.
GLSL은 자체적으로 2,3,4차원 행렬 자료형을 지원한다: mat2 (2x2), mat3 (3x3), mat4 (4x4).
또한, GLSL은 행렬 곱셈(*)을 지원하고 행렬의 성분별 곱셈 함수 (matrixCompMult())도 지원한다.
행렬을 사용하여 벡터 이동도 가능하다.

행렬을 사용하여 좌표계도 회전도 가능하다.
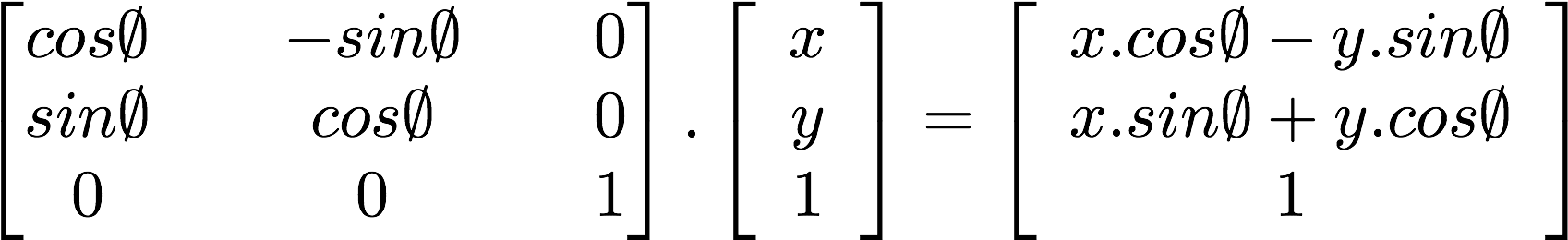
코드로 보자.
vec2(0.0) 지점에서 좌표를 회전한다.
mat2 rotate2d(float _angle){
return mat2(cos(_angle),-sin(_angle),
sin(_angle),cos(_angle));
}
하지만 십자 모양은 vec2(0.0) 위치가 아니다.
캔버스의 중앙인 vec2(0.5) 위치에 있다.
그래서 공간을 회전하기 전, vec2(0.0) 좌표로 이동시킨다.
이후에 회전하고, 다시 원위치 이동한다.

mat2 rotate2d(float _angle){
return mat2(cos(_angle),-sin(_angle),
sin(_angle),cos(_angle));
}
float box(in vec2 _st, in vec2 _size){
// 생략
}
float cross(in vec2 _st, float _size){
// 생략
}
void main(){
vec2 st = gl_FragCoord.xy/u_resolution.xy;
vec3 color = vec3(0.0);
// move space from the center to the vec2(0.0)
st -= vec2(0.5);
// rotate the space
st = rotate2d( sin(u_time)*PI ) * st;
// move it back to the original place
st += vec2(0.5);
// Show the coordinates of the space on the background
// color = vec3(st.x,st.y,0.0);
// Add the shape on the foreground
color += vec3(cross(st,0.4));
gl_FragColor = vec4(color,1.0);
}Scale
행렬을 사용하여 객체의 크기도 조정할 수 있다.

mat2 scale(vec2 _scale){
return mat2(_scale.x,0.0,
0.0,_scale.y);
}


mat2 scale(vec2 _scale){
return mat2(_scale.x,0.0,
0.0,_scale.y);
}
float box(in vec2 _st, in vec2 _size){
// 생략
}
float cross(in vec2 _st, float _size){
// 생략
}
void main(){
vec2 st = gl_FragCoord.xy/u_resolution.xy;
vec3 color = vec3(0.0);
st -= vec2(0.5);
st = scale( vec2(sin(u_time)+1.0) ) * st;
st += vec2(0.5);
// Show the coordinates of the space on the background
// color = vec3(st.x,st.y,0.0);
// Add the shape on the foreground
color += vec3(cross(st,0.2));
gl_FragColor = vec4(color,1.0);
}
// 유의점
회전 행렬과 스케일 행렬 결합시에는 순서가 중요하다.
먼저 행렬을 곱한 다음 벡터를 곱해야한다.
Other uses for matrices: YUV color (행렬의 다른 용도: YUV 색상)
YUV는 색공간이다. (HSB, HSV와 같음)
일반적인 색공간은 RGB이다.
하지만 모든 것을 RGB로 처리하기에는 데이터가 너무 크다.
그래서 고안한게 YUV이다.
크로미넌스 구성 요소의 대역폭을 줄이기 위해,
인간의 인식 범위를 고려한 사진 및 비디오의 아날로그 인코딩에 사용되는 색 공간이다.
다음 코드는 행렬 연산을 사용하여 색상을 변환하는 내용이다.

// YUV to RGB matrix
mat3 yuv2rgb = mat3(1.0, 0.0, 1.13983,
1.0, -0.39465, -0.58060,
1.0, 2.03211, 0.0);
// RGB to YUV matrix
mat3 rgb2yuv = mat3(0.2126, 0.7152, 0.0722,
-0.09991, -0.33609, 0.43600,
0.615, -0.5586, -0.05639);
void main(){
vec2 st = gl_FragCoord.xy/u_resolution;
vec3 color = vec3(0.0);
// UV values goes from -1 to 1
// So we need to remap st (0.0 to 1.0)
st -= 0.5; // becomes -0.5 to 0.5
st *= 2.0; // becomes -1.0 to 1.0
// we pass st as the y & z values of
// a three dimensional vector to be
// properly multiply by a 3x3 matrix
color = yuv2rgb * vec3(0.5, st.x, st.y);
gl_FragColor = vec4(color,1.0);
}위 코드에서는 색상에 행렬을 곱하여 벡터로 처리하고 있다.
이런 식으로 값을 "이동(move)"한다.
// 마치며
도형 컴포지션에 이러한 행렬 연산은 필수이다.
다음 장에서는 이를 이용해 절차적 패턴을 만들 것이다.
반복과 변형을 코딩으로 표현할 것이다.
'셰이더 (Shader) > The Book of Shaders (완)' 카테고리의 다른 글
| [GLSL] 10 - Random (0) | 2023.04.25 |
|---|---|
| [GLSL] 9 - Patterns (0) | 2023.04.20 |
| [GLSL] 7 - Shapes (0) | 2023.04.19 |
| [GLSL] 6 - Colors (0) | 2023.04.18 |
| [GLSL] 5 - Shaping functions (0) | 2023.04.17 |




댓글