
정규화된 좌표계를 3으로 늘린다.
여기에 fract 함수를 적용한다.
0-1값에서 생성된 실수값, 1-2 값에서 생성된 실수값, 2-3 값에서 생성된 실수값.
3x3 셀을 얻을 수 있다.


float circle(in vec2 _st, in float _radius){
vec2 l = _st-vec2(0.5);
return 1.-smoothstep(_radius-(_radius*0.01),
_radius+(_radius*0.01),
dot(l,l)*4.0);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution;
vec3 color = vec3(0.0);
st *= 3.0; // Scale up the space by 3
st = fract(st); // Wrap around 1.0
// Now we have 9 spaces that go from 0-1
color = vec3(st,0.0); // 좌표
color = vec3(circle(st,0.5)); // 동그라미
gl_FragColor = vec4(color,1.0);
}Apply matrices inside patterns
나뉘어진 셀은 정규화된 좌표계의 미니 버전이라고 할 수 있다.
따라서 여기에 행렬 변환을 적용하면 이동, 회전, 크기 조정이 된다.

vec2 rotate2D(vec2 _st, float _angle){
_st -= 0.5;
_st = mat2(cos(_angle),-sin(_angle),
sin(_angle),cos(_angle)) * _st;
_st += 0.5;
return _st;
}
vec2 tile(vec2 _st, float _zoom){
_st *= _zoom;
return fract(_st);
}
float box(vec2 _st, vec2 _size, float _smoothEdges){
_size = vec2(0.5)-_size*0.5;
vec2 aa = vec2(_smoothEdges*0.5);
vec2 uv = smoothstep(_size,_size+aa,_st);
uv *= smoothstep(_size,_size+aa,vec2(1.0)-_st);
return uv.x*uv.y;
}
void main(void){
vec2 st = gl_FragCoord.xy/u_resolution.xy;
vec3 color = vec3(0.0);
// Divide the space in 4
st = tile(st,4.);
// Use a matrix to rotate the space 45 degrees
st = rotate2D(st,PI*0.25);
// Draw a square
color = vec3(box(st,vec2(0.7),0.01));
// color = vec3(st,0.0);
gl_FragColor = vec4(color,1.0);
}Offset patterns
벽돌 벽을 묘사해보자.
벽을 보면 반만큼 벽돌이 오프셋되어 있는 것을 볼 수 있다.

첫 번째로 행이 짝수인지 홀수인지 판별해야한다.
그래야 x를 오프셋할지를 결정할 수 있다.
이를 위해 2.0의 mod()를 사용한 후, 결과가 1.0 미만인지 여부를 확인하면 된다.
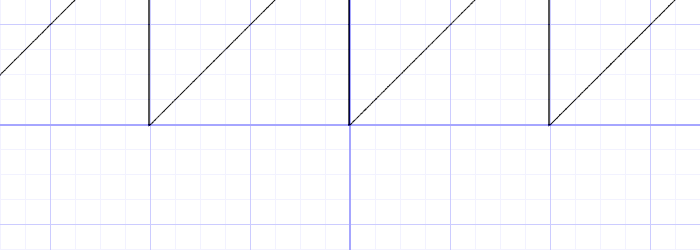

y = mod(x,2.0);
y = mod(x,2.0) < 1.0 ? 0. : 1. ;
y = step(1.0,mod(x,2.0)); // 내장함수 사용보시다시피 삼항 연산자를 사용하여 2.0의 mod()가 1.0 미만(두 번째 줄)인지 확인할 수 있다.
동일한 연산을 수행하지만 더 빠른 step() 함수를 사용할 수도 있다.
// 왜 step함수 사용하는가?
각 그래픽 카드가 코드를 어떻게 최적화하고 컴파일하는지는 알기 어렵다.
그래서 내장 함수가 빠르다고 가정하는 것이 안전하다.
이제 홀수 행에 오프셋을 적용하여 타일에 벽돌 효과를 줄 수 있다.
다음 코드의 14행은 함수를 사용하여 홀수 행을 "감지"하고 x에 반 단위 오프셋을 부여하는 곳이다.
짝수 행의 경우 함수의 결과는 0.0이고 0.0에 오프셋 0.5를 곱하면 0.0의 오프셋이 된다.
그러나 홀수 행에서는 함수 결과인 1.0에 오프셋 0.5를 곱하면 좌표계의 x축이 0.5만큼 이동한다.

vec2 brickTile(vec2 _st, float _zoom){
_st *= _zoom;
// Here is where the offset is happening
_st.x += step(1., mod(_st.y,2.0)) * 0.5;
return fract(_st);
}
float box(vec2 _st, vec2 _size){
_size = vec2(0.5)-_size*0.5;
vec2 uv = smoothstep(_size,_size+vec2(1e-4),_st);
uv *= smoothstep(_size,_size+vec2(1e-4),vec2(1.0)-_st);
return uv.x*uv.y;
}
void main(void){
vec2 st = gl_FragCoord.xy/u_resolution.xy;
vec3 color = vec3(0.0);
// Modern metric brick of 215mm x 102.5mm x 65mm
// http://www.jaharrison.me.uk/Brickwork/Sizes.html
// st /= vec2(2.15,0.65)/1.5;
// Apply the brick tiling
st = brickTile(st,5.0);
color = vec3(box(st,vec2(0.9)));
// Uncomment to see the space coordinates
//color = vec3(st,0.0);
gl_FragColor = vec4(color,1.0);
}Truchet Tiles
현재 셀이 짝수 행 또는 열에 있는지, 홀수 행 또는 열에 있는지 구분하는 방법을 배웠다.
위치에 따라 하나의 형태를 다르게 표현할 수 있다.


공간을 4개의 셀로 분할하고,
각 셀에 회전 각도를 할당하는 rotateTilePattern() 함수에 주목해라.

vec2 rotate2D (vec2 _st, float _angle) {
_st -= 0.5;
_st = mat2(cos(_angle),-sin(_angle),
sin(_angle),cos(_angle)) * _st;
_st += 0.5;
return _st;
}
vec2 tile (vec2 _st, float _zoom) {
_st *= _zoom;
return fract(_st);
}
vec2 rotateTilePattern(vec2 _st){
// Scale the coordinate system by 2x2
_st *= 2.0;
// Give each cell an index number
// according to its position
float index = 0.0;
index += step(1., mod(_st.x,2.0));
index += step(1., mod(_st.y,2.0))*2.0;
// |
// 2 | 3
// |
//--------------
// |
// 0 | 1
// |
// Make each cell between 0.0 - 1.0
_st = fract(_st);
// Rotate each cell according to the index
if(index == 1.0){
// Rotate cell 1 by 90 degrees
_st = rotate2D(_st,PI*0.5);
} else if(index == 2.0){
// Rotate cell 2 by -90 degrees
_st = rotate2D(_st,PI*-0.5);
} else if(index == 3.0){
// Rotate cell 3 by 180 degrees
_st = rotate2D(_st,PI);
}
return _st;
}
void main (void) {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st = tile(st,3.0);
st = rotateTilePattern(st);
gl_FragColor = vec4(vec3(step(st.x,st.y)),1.0);
}
'셰이더 (Shader) > The Book of Shaders (완)' 카테고리의 다른 글
| [GLSL] 11 - Noise (0) | 2023.04.26 |
|---|---|
| [GLSL] 10 - Random (0) | 2023.04.25 |
| [GLSL] 8 - 2D Matrices (1) | 2023.04.20 |
| [GLSL] 7 - Shapes (0) | 2023.04.19 |
| [GLSL] 6 - Colors (0) | 2023.04.18 |




댓글