
현실 세계 무작위성을 가지고 있지만, 랜덤과는 다르다.
이 다양성을 어떻게 표현할까?
1980년대 초 영화 "트론"을 위해 보다 사실적인 텍스처를 생성해 달라는 의뢰를 받은 켄 펄린은 이 문제를 해결했다.
이에 대한 해답으로 노이즈 알고리즘을 고안해냈다.
다음은 고전적인 펄린 노이즈 알고리즘은 아니지만, 노이즈 생성 방법을 이해하기 위한 기초 예제이다.
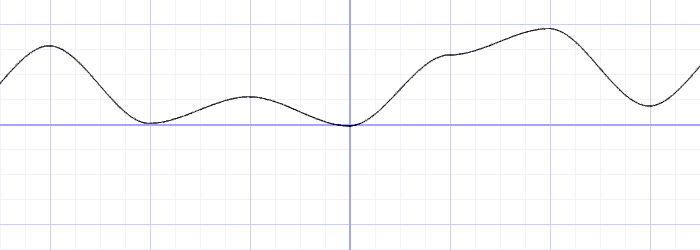
float i = floor(x); // integer
float f = fract(x); // fraction
y = rand(i); //rand() is described in the previous chapter
y = mix(rand(i), rand(i + 1.0), f); // 선형 보간법
y = mix(rand(i), rand(i + 1.0), smoothstep(0.,1.,f)); // 스무스한 보간법이전 장에서 했던 것과 비슷한 작업을 한다.
- 연속된 float 값(x)을 정수(i)와 소수점 이하(f)로 나눈다.
floor()를 사용하여 i를 구한다. fract()를 사용하여 f를 구한다.
- 그 다음 i에 rand()를 적용한다.
각 정수에 대해 랜덤 값이 부여된다.
- 그 후, 랜덤값을 선형적으로 보간한다.
선형 보간 대신 smoothstep()을 이용해 보간하면 부드러운 결과가 나온다.
2D Noise

여기까지 1D에서 노이즈를 보간하는 방법을 알아보았다.
2D로 넘어갈 차례이다.
2D에서는 선의 두 점 사이를 보간하지 않는다.
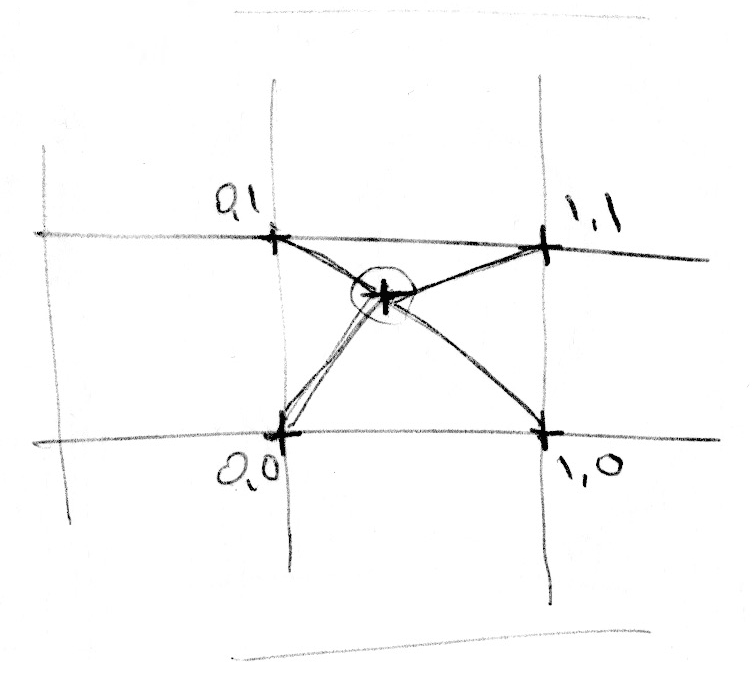
대신에 평면의 정사각형 영역의 네 모서리 사이를 보간한다.
- 두 점 사이 보간
rand(x)
rand(x) + 1.0
- 네 모서리 보간
rand(st)
rand(st) + vec2(1.0, 0.0)
rand(st) + vec2(0.0, 1.0)
rand(st) + vec2(1.0, 1.0)
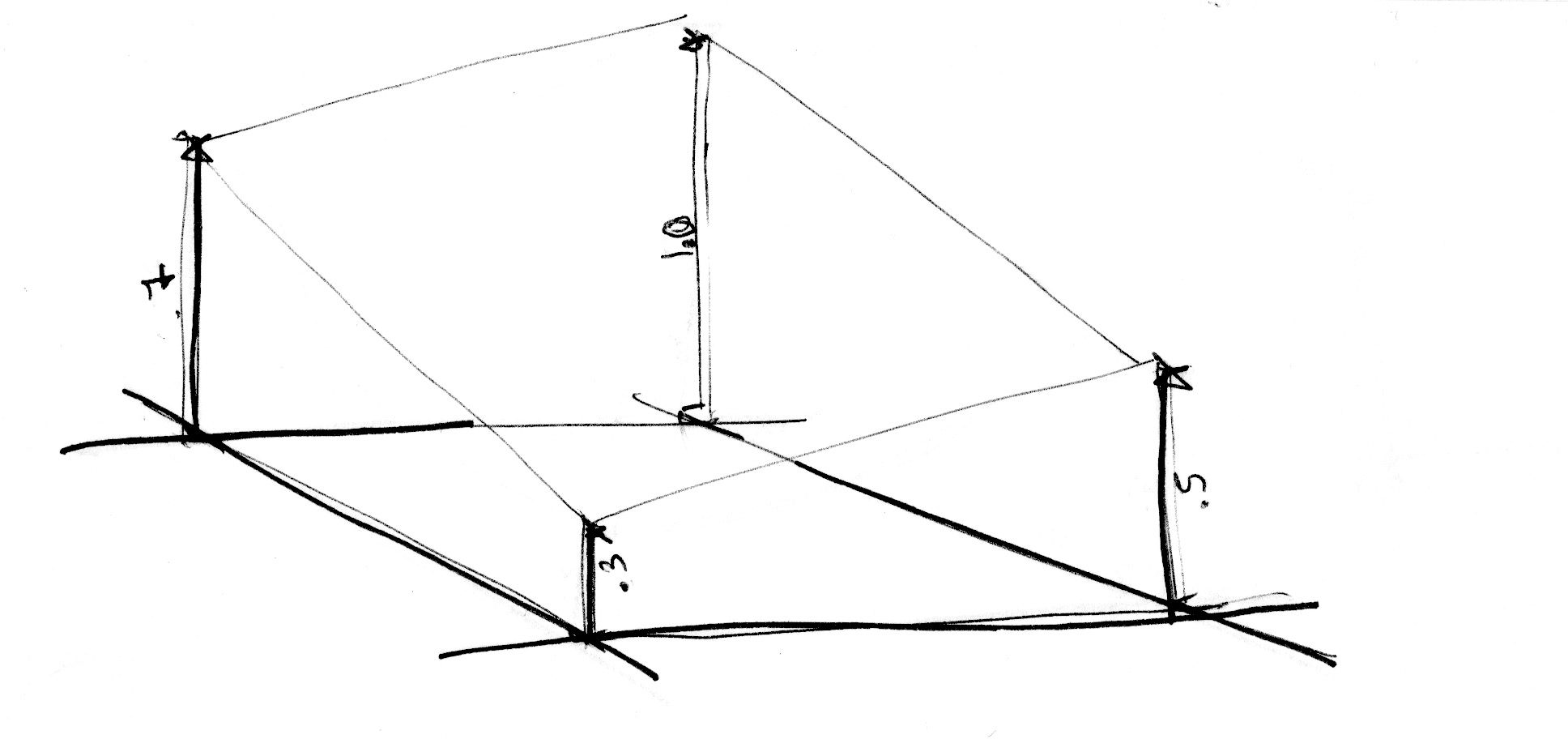
마찬가지로 3D 노이즈를 얻으려면 큐브의 여덟 모서리 사이를 보간해야 한다.
이 기술은 임의의 값을 보간하는 것이다.
이를 value 노이즈라고 한다.
1D 노이즈 예시와 마찬가지로 부드럽게 보간하는 cubic 보간(smoothstep)을 적용하면 다음과 같다.

코드 예제를 살펴보자.

// 2D Random
float random (in vec2 st) {
return fract(sin(dot(st.xy,
vec2(12.9898,78.233)))
* 43758.5453123);
}
float noise (in vec2 st) {
vec2 i = floor(st);
vec2 f = fract(st);
// Four corners in 2D of a tile
float a = random(i);
float b = random(i + vec2(1.0, 0.0));
float c = random(i + vec2(0.0, 1.0));
float d = random(i + vec2(1.0, 1.0));
// Smooth Interpolation
// Cubic Hermine Curve. Same as SmoothStep()
vec2 u = f*f*(3.0-2.0*f);
// u = smoothstep(0.,1.,f);
// Mix 4 coorners percentages
return mix(a, b, u.x) +
(c - a)* u.y * (1.0 - u.x) +
(d - b) * u.x * u.y;
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
// Scale the coordinate system to see
// some noise in action
vec2 pos = vec2(st*5.0);
// Use the noise function
float n = noise(pos);
gl_FragColor = vec4(vec3(n), 1.0);
}좌표를 5로 곱한다.
// noise 함수
함수 내에서 좌표를 셀로 분할한다.
셀의 정수 위치(i)와 셀 내부의 소수점 아래(f)를 변수에 담는다.
정수 위치를 사용하여 네 모서리의 좌표를 계산한다.
각 모서리에 대한 임의의 값을 얻는다.
소수점 아래 값을 사용하여 모서리의 임의의 값 4개를 보간한다.
Using Noise in Generative Designs
노이즈 알고리즘은 원래 디지털 텍스처에 자연스러운 느낌을 주기 위해 고안되었다.
지금까지 살펴본 1D, 2D 구현은 랜덤한 값 사이의 보간이었다.
이를 Value 노이즈라고 부른다.
하지만 노이즈를 얻는 방법에는 더 많은 방법이 있다.
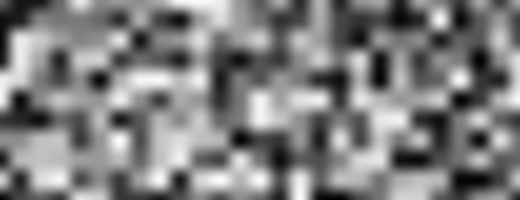
Value 노이즈는 블록처럼 보이는 경향이 있다.
이러한 블록 효과를 줄이기 위해 1985년 Ken Perlin은 Gradient 노이즈라는 알고리즘을 개발했다.
Ken은 값 대신 랜덤한 gradient를 보간하는 방법을 알아냈다.
이러한 gradient는 단일 값(float) 대신 방향(vec2로 표시)을 반환하는 2D 랜덤 함수의 결과이다.

vec2 random2(vec2 st){
st = vec2( dot(st,vec2(127.1,311.7)),
dot(st,vec2(269.5,183.3)) );
return -1.0 + 2.0*fract(sin(st)*43758.5453123);
}
float noise(vec2 st) {
vec2 i = floor(st);
vec2 f = fract(st);
vec2 u = f*f*(3.0-2.0*f);
return mix( mix( dot( random2(i + vec2(0.0,0.0) ), f - vec2(0.0,0.0) ),
dot( random2(i + vec2(1.0,0.0) ), f - vec2(1.0,0.0) ), u.x),
mix( dot( random2(i + vec2(0.0,1.0) ), f - vec2(0.0,1.0) ),
dot( random2(i + vec2(1.0,1.0) ), f - vec2(1.0,1.0) ), u.x), u.y);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(0.0);
vec2 pos = vec2(st*10.0);
color = vec3( noise(pos)*.5+.5 );
gl_FragColor = vec4(color,1.0);
}
노이즈 구현에 대해 더 많이 알수록 마치 화가처럼 더 잘 사용할 수 있다.
예를 들어 2차원 노이즈 구현시 좌표를 회전하면 나무결 같은 느낌을 만들 수 있다.

float random (in vec2 st) {
return fract(sin(dot(st.xy,
vec2(12.9898,78.233)))
* 43758.5453123);
}
float noise(vec2 st) {
vec2 i = floor(st);
vec2 f = fract(st);
vec2 u = f*f*(3.0-2.0*f);
return mix( mix( random( i + vec2(0.0,0.0) ),
random( i + vec2(1.0,0.0) ), u.x),
mix( random( i + vec2(0.0,1.0) ),
random( i + vec2(1.0,1.0) ), u.x), u.y);
}
mat2 rotate2d(float angle){
return mat2(cos(angle),-sin(angle),
sin(angle),cos(angle));
}
float lines(in vec2 pos, float b){
float scale = 10.0;
pos *= scale;
return smoothstep(0.0,
.5+b*.5,
abs((sin(pos.x*3.1415)+b*2.0))*.5);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.y *= u_resolution.y/u_resolution.x;
vec2 pos = st.yx*vec2(10.,3.);
float pattern = pos.x;
// Add noise
pos = rotate2d( noise(pos) ) * pos;
// Draw lines
pattern = lines(pos,.5);
gl_FragColor = vec4(vec3(pattern),1.0);
}
노이즈에서 흥미로운 패턴을 얻는 또 다른 방법도 있다.
노이즈를 디스턴스 필드처럼 취급하는 것이다.
이것은 shapes 챕터에서 설명한 몇 가지 트릭을 적용하는 것이다.

vec2 random2(vec2 st){
st = vec2( dot(st,vec2(127.1,311.7)),
dot(st,vec2(269.5,183.3)) );
return -1.0 + 2.0*fract(sin(st)*43758.5453123);
}
float noise(vec2 st) {
vec2 i = floor(st);
vec2 f = fract(st);
vec2 u = f*f*(3.0-2.0*f);
return mix( mix( dot( random2(i + vec2(0.0,0.0) ), f - vec2(0.0,0.0) ),
dot( random2(i + vec2(1.0,0.0) ), f - vec2(1.0,0.0) ), u.x),
mix( dot( random2(i + vec2(0.0,1.0) ), f - vec2(0.0,1.0) ),
dot( random2(i + vec2(1.0,1.0) ), f - vec2(1.0,1.0) ), u.x), u.y);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(0.0);
float t = 1.0;
// Uncomment to animate
// t = abs(1.0-sin(u_time*.1))*5.;
// Comment and uncomment the following lines:
st += noise(st*2.)*t; // Animate the coordinate space
color = vec3(1.) * smoothstep(.18,.2,noise(st)); // Big black drops
color += smoothstep(.15,.2,noise(st*10.)); // Black splatter
color -= smoothstep(.35,.4,noise(st*10.)); // Holes on splatter
gl_FragColor = vec4(1.-color,1.0);
}
노이즈 함수를 사용하는 세 번째 방법은 도형을 변형하는 것이다.
이 역시 shapes챕터에서 배운 몇 가지 기술이 필요하다.

vec2 random2(vec2 st){
st = vec2( dot(st,vec2(127.1,311.7)),
dot(st,vec2(269.5,183.3)) );
return -1.0 + 2.0*fract(sin(st)*43758.5453123);
}
float noise(vec2 st) {
vec2 i = floor(st);
vec2 f = fract(st);
vec2 u = f*f*(3.0-2.0*f);
return mix( mix( dot( random2(i + vec2(0.0,0.0) ), f - vec2(0.0,0.0) ),
dot( random2(i + vec2(1.0,0.0) ), f - vec2(1.0,0.0) ), u.x),
mix( dot( random2(i + vec2(0.0,1.0) ), f - vec2(0.0,1.0) ),
dot( random2(i + vec2(1.0,1.0) ), f - vec2(1.0,1.0) ), u.x), u.y);
}
mat2 rotate2d(float _angle){
return mat2(cos(_angle),-sin(_angle),
sin(_angle),cos(_angle));
}
float shape(vec2 st, float radius) {
st = vec2(0.5)-st;
float r = length(st)*2.0;
float a = atan(st.y,st.x);
float m = abs(mod(a+u_time*2.,3.14*2.)-3.14)/3.6;
float f = radius;
m += noise(st+u_time*0.1)*.5;
// a *= 1.+abs(atan(u_time*0.2))*.1;
// a *= 1.+noise(st+u_time*0.1)*0.1;
f += sin(a*50.)*noise(st+u_time*.2)*.1;
f += (sin(a*20.)*.1*pow(m,2.));
return 1.-smoothstep(f,f+0.007,r);
}
float shapeBorder(vec2 st, float radius, float width) {
return shape(st,radius)-shape(st,radius-width);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
vec3 color = vec3(1.0) * shapeBorder(st,0.8,0.02);
gl_FragColor = vec4( 1.-color, 1.0 );
}
// 실습 과제
움직임에 노이즈를 적용하는 것도 좋은 방법이다.
Matrices 챕터로 돌아가보라.
"+"로 이동하는 translate 예제를 사용하여 랜덤과 노이즈 움직임을 적용해보라.
Improved Noise
펄린은 개선된 노이즈를 발표했다.
이 원리는, cubic Hermite curve (f(x) = 3x^2-2x^3 , smoothstep() 함수와 동일)이었던 것을,
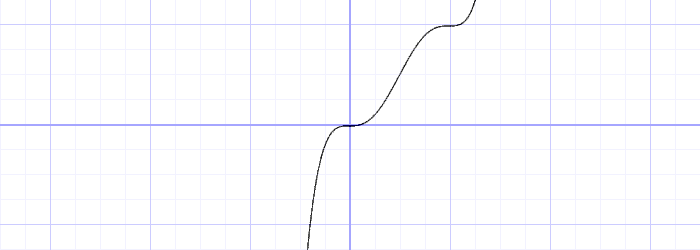
quintic interpolation curve(f(x) = 6x^5-15x^4+10x^3 )으로 대체한 것이다.
이렇게 하면 커브의 양쪽 끝이 더 평평해져서 각 테두리가 다음 테두리와 부드럽게 이어진다.
즉, 셀 간에 보다 연속적인 전환을 얻을 수 있다.
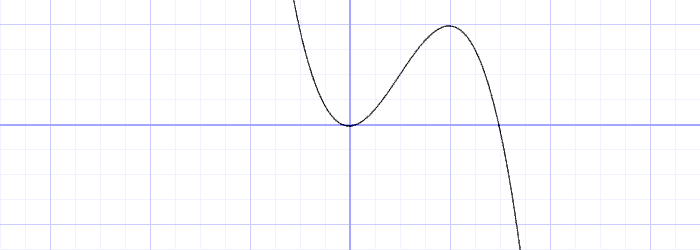
// Cubic Hermite Curve. Same as SmoothStep() (좌측 이미지)
y = x*x*(3.0-2.0*x);
// Quintic interpolation curve (우측 이미지)
y = x*x*x*(x*(x*6.-15.)+10.);Simplex Noise
켄 펄린은 알고리즘의 성공만으로는 충분하지 않았다.
그는 더 나은 성능을 내도록 개선하였다.
그는 시그래프 2001에서 이전 알고리즘보다 나은 개선된 심플렉스 노이즈를 발표했다.
- 계산 복잡도가 낮고 곱셈 횟수가 적은 알고리즘.
- 적은 계산 비용으로 더 높은 차원으로 확장되는 노이즈.
- 방향성 아티팩트가 없는 노이즈.
- 상당히 저렴하게 계산할 수 있는 잘 정의되고 연속적인 그라디언트를 갖는 노이즈다.
- 하드웨어에서 구현하기 쉬운 알고리즘.
어떻게 알고리즘을 개선하였을까?
우리는 2차원에서 4점(사각형의 꼭짓점)을 보간하는 방법을 배웠다.
그러므로, 3차원과 4차원의 경우, 8점과 16점을 보간해야 한다고 추측할 수 있다.
즉, N차원의 경우, 2에서 N점(2^N)까지 부드럽게 보간해야 한다.
그러나 Ken은 공간을 채울 수 있는 확실한 모양은 정사각형이지만,
2차원에서 가장 간단한 모양은 정삼각형이라는 것을 알게 되었다.
그래서 그는 정사각 그리드를 정삼각형의 심플렉스 그리드로 교체하였다.
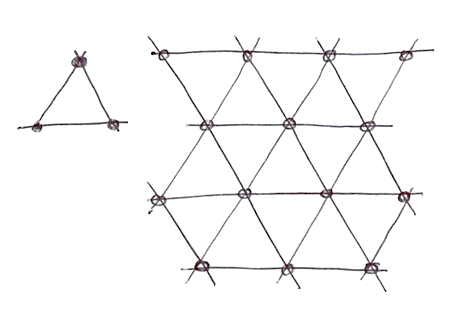
N 차원 심플렉스 도형은 N + 1개의 꼭짓점이 있다.
즉, 2D로 계산할 때 한 꼭짓점 적게,
3D일때는 네 꼭짓점 적게,
4D일때는 11개의 꼭짓점이 적다.
비용 절감이 된다.
// 심플렉스 그리드 만들기 (삼각형)
심플렉스 그리드는 어떻게 만드는가?
그 방법은 모서리 4개 그리드의 셀을 두 개의 이등변 삼각형으로 나눈다.
그리고 삼각형이 등변이 될 때까지 기울이면 구할 수 있다.
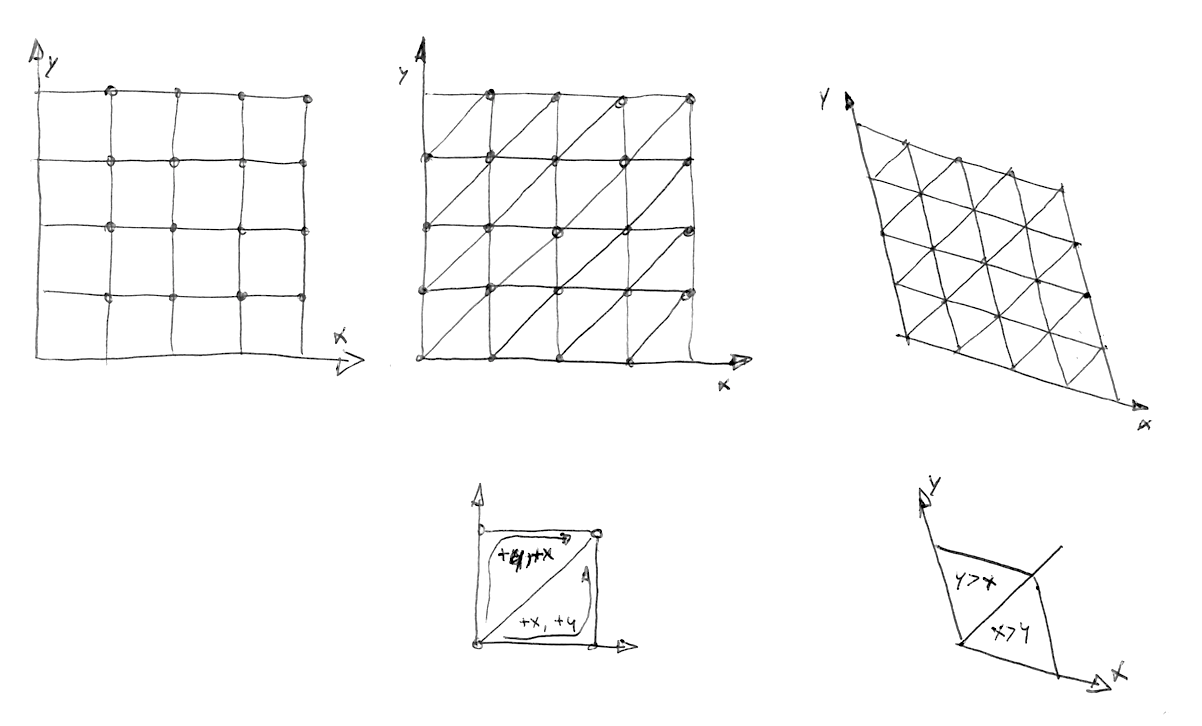
스테판 구스타브슨의 논문을 보면 다음과 같이 설명한다.
계산하고싶은 지점의 정수로 변환된 좌표(x,y)를 보라.
두 개의 도형 중 어느 셀이 그 점을 포함하는지 알 수 있다.
x와 y의 크기를 비교하여, 점이 상단 심플렉스인지 하단 심플렉스인지 파악한다.
세 개의 정확한 꼭짓점을 횡단하여 자른다.
다음 코드를 보자.
그리드가 어떻게 기울어졌는지 확인해보라.
심플렉스 그리드를 구성하는 방법을 확인할 수 있다.
y("아래쪽" 삼각형) 또는 y > x("위쪽" 삼각형)를 감지하여, 기울어진 사각형을 두 개의 정삼각형으로 분할하는 방법에 유의하라.


vec2 skew (vec2 st) {
vec2 r = vec2(0.0);
r.x = 1.1547*st.x;
r.y = st.y+0.5*r.x;
return r;
}
vec3 simplexGrid (vec2 st) {
vec3 xyz = vec3(0.0);
vec2 p = fract(skew(st));
if (p.x > p.y) {
xyz.xy = 1.0-vec2(p.x,p.y-p.x);
xyz.z = p.y;
} else {
xyz.yz = 1.0-vec2(p.x-p.y,p.y);
xyz.x = p.x;
}
return fract(xyz);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
vec3 color = vec3(0.0);
// Scale the space to see the grid
st *= 10.;
// Show the 2D grid
color.rg = fract(st);
// Skew the 2D grid
color.rg = fract(skew(st));
// Subdivide the grid into to equilateral triangles
color = simplexGrid(st);
gl_FragColor = vec4(color,1.0);
}
simplex noise를 GLSL에서 구현한 것을 보자.
McEwan와 Stefan Gustavson이 만든 예제이다.

// Some useful functions
vec3 mod289(vec3 x) { return x - floor(x * (1.0 / 289.0)) * 289.0; }
vec2 mod289(vec2 x) { return x - floor(x * (1.0 / 289.0)) * 289.0; }
vec3 permute(vec3 x) { return mod289(((x*34.0)+1.0)*x); }
float snoise(vec2 v) {
// Precompute values for skewed triangular grid
const vec4 C = vec4(0.211324865405187,
// (3.0-sqrt(3.0))/6.0
0.366025403784439,
// 0.5*(sqrt(3.0)-1.0)
-0.577350269189626,
// -1.0 + 2.0 * C.x
0.024390243902439);
// 1.0 / 41.0
// First corner (x0)
vec2 i = floor(v + dot(v, C.yy));
vec2 x0 = v - i + dot(i, C.xx);
// Other two corners (x1, x2)
vec2 i1 = vec2(0.0);
i1 = (x0.x > x0.y)? vec2(1.0, 0.0):vec2(0.0, 1.0);
vec2 x1 = x0.xy + C.xx - i1;
vec2 x2 = x0.xy + C.zz;
// Do some permutations to avoid
// truncation effects in permutation
i = mod289(i);
vec3 p = permute(
permute( i.y + vec3(0.0, i1.y, 1.0))
+ i.x + vec3(0.0, i1.x, 1.0 ));
vec3 m = max(0.5 - vec3(
dot(x0,x0),
dot(x1,x1),
dot(x2,x2)
), 0.0);
m = m*m ;
m = m*m ;
// Gradients:
// 41 pts uniformly over a line, mapped onto a diamond
// The ring size 17*17 = 289 is close to a multiple
// of 41 (41*7 = 287)
vec3 x = 2.0 * fract(p * C.www) - 1.0;
vec3 h = abs(x) - 0.5;
vec3 ox = floor(x + 0.5);
vec3 a0 = x - ox;
// Normalise gradients implicitly by scaling m
// Approximation of: m *= inversesqrt(a0*a0 + h*h);
m *= 1.79284291400159 - 0.85373472095314 * (a0*a0+h*h);
// Compute final noise value at P
vec3 g = vec3(0.0);
g.x = a0.x * x0.x + h.x * x0.y;
g.yz = a0.yz * vec2(x1.x,x2.x) + h.yz * vec2(x1.y,x2.y);
return 130.0 * dot(m, g);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(0.0);
// Scale the space in order to see the function
st *= 10.;
color = vec3(snoise(st)*.5+.5);
gl_FragColor = vec4(color,1.0);
}
마지막으로 응용 예제를 살펴보자.

vec3 mod289(vec3 x) { return x - floor(x * (1.0 / 289.0)) * 289.0; }
vec2 mod289(vec2 x) { return x - floor(x * (1.0 / 289.0)) * 289.0; }
vec3 permute(vec3 x) { return mod289(((x*34.0)+1.0)*x); }
float snoise(vec2 v) {
const vec4 C = vec4(0.211324865405187, // (3.0-sqrt(3.0))/6.0
0.366025403784439, // 0.5*(sqrt(3.0)-1.0)
-0.577350269189626, // -1.0 + 2.0 * C.x
0.024390243902439); // 1.0 / 41.0
vec2 i = floor(v + dot(v, C.yy) );
vec2 x0 = v - i + dot(i, C.xx);
vec2 i1;
i1 = (x0.x > x0.y) ? vec2(1.0, 0.0) : vec2(0.0, 1.0);
vec4 x12 = x0.xyxy + C.xxzz;
x12.xy -= i1;
i = mod289(i); // Avoid truncation effects in permutation
vec3 p = permute( permute( i.y + vec3(0.0, i1.y, 1.0 ))
+ i.x + vec3(0.0, i1.x, 1.0 ));
vec3 m = max(0.5 - vec3(dot(x0,x0), dot(x12.xy,x12.xy), dot(x12.zw,x12.zw)), 0.0);
m = m*m ;
m = m*m ;
vec3 x = 2.0 * fract(p * C.www) - 1.0;
vec3 h = abs(x) - 0.5;
vec3 ox = floor(x + 0.5);
vec3 a0 = x - ox;
m *= 1.79284291400159 - 0.85373472095314 * ( a0*a0 + h*h );
vec3 g;
g.x = a0.x * x0.x + h.x * x0.y;
g.yz = a0.yz * x12.xz + h.yz * x12.yw;
return 130.0 * dot(m, g);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(0.0);
vec2 pos = vec2(st*3.);
float DF = 0.0;
// Add a random position
float a = 0.0;
vec2 vel = vec2(u_time*.1);
DF += snoise(pos+vel)*.25+.25;
// Add a random position
a = snoise(pos*vec2(cos(u_time*0.15),sin(u_time*0.1))*0.1)*3.1415;
vel = vec2(cos(a),sin(a));
DF += snoise(pos+vel)*.25+.25;
color = vec3( smoothstep(.7,.75,fract(DF)) );
gl_FragColor = vec4(1.0-color,1.0);
}
'셰이더 (Shader) > The Book of Shaders (완)' 카테고리의 다른 글
| [GLSL] 13 - Fractal Brownian Motion (0) | 2023.05.04 |
|---|---|
| [GLSL] 12 - Cellular Noise (0) | 2023.05.03 |
| [GLSL] 10 - Random (0) | 2023.04.25 |
| [GLSL] 9 - Patterns (0) | 2023.04.20 |
| [GLSL] 8 - 2D Matrices (1) | 2023.04.20 |




댓글