
펄린의 노이즈가 나온 지 16년 후이자,
심플렉스 노이즈가 나오기 5년 전인 1996년, 스티븐 월리는 "셀룰러 텍스처 베이스 함수"라는 논문을 썼다.
이 기법의 원리를 이해하려면 반복문에 대해 알아야한다.
GLSL에서 for 루프에는 단점이 있다.
조건식의 숫자가 상수(const)여야 한다는 점이다.
따라서 동적 루프는 사용할 수 없다. 반복 횟수를 고정해야한다.
예제를 보자.
Points for a distance field
셀룰러 노이즈는 거리 필드 기반으로 계산한다.
특정한 점으로부터의 가장 가까운 지점까지의 거리를 사용하는 것이다.
예를 들어, 4개의 점으로 구성된 거리 필드를 만들어보자.
각 픽셀이 가장 가까운 점까지의 거리를 계산해야한다.
즉, 점 개수만큼 반복하여 현재 픽셀까지의 거리를 계산한다.
이후 가장 가까운 점을 찾아 거리 값을 저장해야한다.
float min_dist = 100.; // A variable to store the closest distance to a point
min_dist = min(min_dist, distance(st, point_a));
min_dist = min(min_dist, distance(st, point_b));
min_dist = min(min_dist, distance(st, point_c));
min_dist = min(min_dist, distance(st, point_d));
배열과 for 루프를 사용해 다시 구현해보자.
float m_dist = 100.; // minimum distance
for (int i = 0; i < TOTAL_POINTS; i++) {
float dist = distance(st, points[i]);
m_dist = min(m_dist, dist);
}
for 루프를 사용하여 점 배열을 반복한다.
min() 함수를 사용하여 최소 거리를 얻는 방법에 주목하라. 예제를 보자.

void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(.0);
// Cell positions
vec2 point[5];
point[0] = vec2(0.83,0.75);
point[1] = vec2(0.60,0.07);
point[2] = vec2(0.28,0.64);
point[3] = vec2(0.31,0.26);
point[4] = u_mouse/u_resolution;
float m_dist = 1.; // minimum distance
// Iterate through the points positions
for (int i = 0; i < 5; i++) {
float dist = distance(st, point[i]);
// Keep the closer distance
m_dist = min(m_dist, dist);
}
// Draw the min distance (distance field)
color += m_dist;
// Show isolines
// color -= step(.7,abs(sin(50.0*m_dist)))*.3;
gl_FragColor = vec4(color,1.0);
}위 코드에서는 점들 중에 하나가 마우스 위치에 할당되어있다.
Tiling and iteration
루프와 배열은 GLSL에 그다지 좋은 방법이 아니다.
앞서 말했듯이 루프는 동적으로 동작하지 않는다.
또한 많이 반복하면 셰이더의 성능이 크게 저하된다.
즉, 많은 양의 점이 필요할 때는 이 방식을 사용할 수 없다.
GPU의 병렬 처리 아키텍처를 활용하는 다른 전략을 찾을 필요가 있다.

이 문제에 접근하는 한 가지 방법은 공간을 타일로 나누는 것이다.
모든 픽셀이 모든 지점까지의 거리를 확인할 필요는 없다.
픽셀의 좌표를 셀로 나눌 수 있다. 각 셀은 하나의 고유한 점을 만들 수 있다.
또한 셀과 셀 사이의 가장자리에 경계가 나타나는 것을 피하려면 인접한 셀의 점까지의 거리를 확인해야한다.
이것이 바로 스티븐 월리의 논문의 주요 아이디어이다.
결국 각 픽셀은 자신의 셀의 점과 주변 8개 셀의 점, 즉 9개의 위치만 확인하면 된다.
이미 좌표를 셀로 나누는 것은 이전 장들에서 해본 것들이므로 익숙할 것이다.
// Scale
st *= 3.;
// Tile the space
vec2 i_st = floor(st);
vec2 f_st = fract(st);
이제 i_st(정수 좌표)를 사용하여 임의의 점 위치를 만든다.
우리가 사용할 random2f 함수는 vec2를 받아 임의의 위치를 가진 vec2를 반환한다.
따라서 각 타일마다 임의의 점 하나가 생긴다.
vec2 point = random2(i_st);이제 각 픽셀은 위에서 만든 점까지의 거리값을 구한다.
vec2 diff = point - f_st;
float dist = length(diff);결과는 다음과 같다.

현재 타일에 있는 점뿐만 아니라, 주변 타일의 점까지의 거리도 확인해야한다.
이를 위해 이웃 타일 개수도 포함하여 반복해야한다.
X축에서는 -1(왼쪽)에서 1(오른쪽) 타일까지
Y축에서는 -1(아래쪽)에서 1(위쪽)까지가 대상이 된다.
9개의 타일로 구성된 3x3 영역은 이와 같은 이중 for 루프를 사용하여 반복할 수 있다.
for (int y= -1; y <= 1; y++) {
for (int x= -1; x <= 1; x++) {
// Neighbor place in the grid
vec2 neighbor = vec2(float(x),float(y));
...
}
}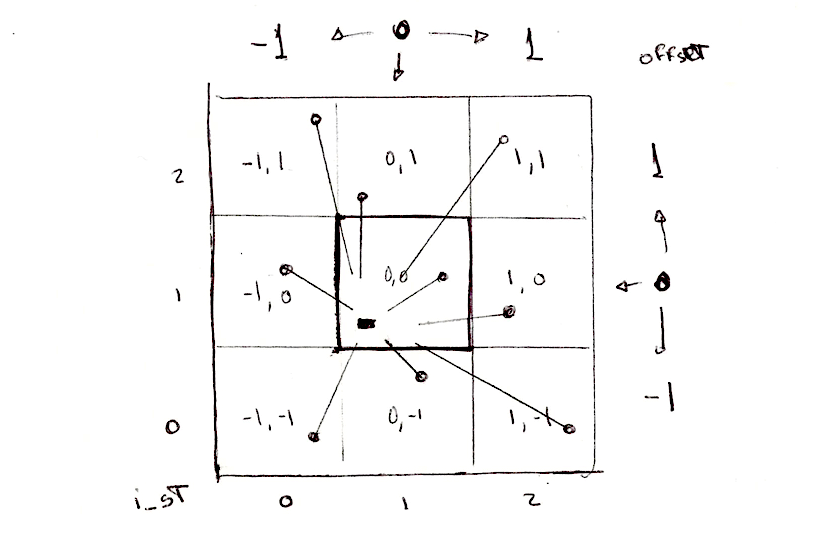
원리는 현재 타일 좌표에 이웃 타일 오프셋을 추가하는 것이다.
이러면 이웃 타일의 점의 위치를 계산할 수 있다.
...
// Random position from current + neighbor place in the grid
vec2 point = random2(i_st + neighbor);
...이후에는 점까지의 거리를 계산하고,
가장 가까운 거리(최소 거리)를 m_dist라는 변수에 저장한다.
...
vec2 diff = neighbor + point - f_st;
// Distance to the point
float dist = length(diff);
// Keep the closer distance
m_dist = min(m_dist, dist);
...
또한 훌륭한 팁이 있다는 점을 주목하라.
대부분 원점에서 도메인공간(월드 또는 오브젝트 공간)에서 임의의 점을 생성한다.
그래서 정밀도 문제로 어려움을 겪는다.
이를 해결하고자 코드를 더 높은 정밀도의 데이터 유형으로 변경하는 방법을 사용한다.
하지만 예제 코드에서는 점을 도메인 공간에서 생성하지 않고 셀 공간에서 생성한다.
정수와 소수점 아래를 추출하여 작업 중인 셀을 식별하고 이 셀 주변에서 일어나는 곳에만 접근한다.
따라서 좌표의 정수 부분은 모두 삭제해도 되므로, 많은 비트를 절약할 수 있다.
비용을 지불하지 않고도 floor() 및 fract() 계산을 수행한 다음 나머지 계산을 부동 소수점으로 처리할 수 있다.
물론 펄린 노이즈 패턴에도 이러한 팁을 적용할 수 있다.
요약하면,
1. 공간을 타일로 나눈다.
2. 각 픽셀이 자신의 타일과 주변 8개의 타일에 있는 지점까지의 거리를 계산한다.
3. 가장 가까운 거리를 저장한다.
4. 다음 예제와 같은 거리 필드가 생성된다.

vec2 random2( vec2 p ) {
return fract(sin(vec2(dot(p,vec2(127.1,311.7)),dot(p,vec2(269.5,183.3))))*43758.5453);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(.0);
// Scale
st *= 3.;
// Tile the space
vec2 i_st = floor(st);
vec2 f_st = fract(st);
float m_dist = 1.; // minimum distance
for (int y= -1; y <= 1; y++) {
for (int x= -1; x <= 1; x++) {
// Neighbor place in the grid
vec2 neighbor = vec2(float(x),float(y));
// Random position from current + neighbor place in the grid
vec2 point = random2(i_st + neighbor);
// Animate the point
point = 0.5 + 0.5*sin(u_time + 6.2831*point);
// Vector between the pixel and the point
vec2 diff = neighbor + point - f_st;
// Distance to the point
float dist = length(diff);
// Keep the closer distance
m_dist = min(m_dist, dist);
}
}
// Draw the min distance (distance field)
color += m_dist;
// Draw cell center
color += 1.-step(.02, m_dist);
// Draw grid
color.r += step(.98, f_st.x) + step(.98, f_st.y);
// Show isolines
// color -= step(.7,abs(sin(27.0*m_dist)))*.5;
gl_FragColor = vec4(color,1.0);
}
이 알고리즘을 픽셀이 아닌 포인트의 관점에서 해석해보자.
각 포인트가 차지할 수 있는 최대 영역은 다른 포인트가 차지한 영역 바로전이다. (콜리전)
이는 자연의 성장 규칙과 같다.
생명체는 확장하고 성장하려는 힘이 있고, 외부의 힘과의 긴장에 의해 최종적인 모양이 형성된다.
이를 시뮬레이션하는 알고리즘 이름은 게오르기 보로노이라는 학자의 이름을 따서 지어졌다.

Voronoi Algorithm
셀룰러 노이즈를 활용해 보로노이를 만드는 것은 생각보다 어렵지 않다.
픽셀에 가장 가까운 정확한 지점에 대한 추가 정보를 보관하면 된다.
이를 위해 m_point라는 vec2를 사용한다.
거리 대신 가장 가까운 점의 중심에 대한 벡터 방향을 저장하는 것이다.
...
if( dist < m_dist ) {
m_dist = dist;
m_point = point;
}
...
다음 코드에서는 더 이상 최소값을 사용하여 가장 가까운 거리를 계산하지 않는다.
대신에 if 문을 사용하고 있다.
왜 그럴까?
새로운 가까운 지점이 있을 때마다 그 위치를 저장할 것이기 때문이다.

void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(.0);
// Cell positions
vec2 point[5];
point[0] = vec2(0.83,0.75);
point[1] = vec2(0.60,0.07);
point[2] = vec2(0.28,0.64);
point[3] = vec2(0.31,0.26);
point[4] = u_mouse/u_resolution;
float m_dist = 1.; // minimum distance
vec2 m_point; // minimum position
// Iterate through the points positions
for (int i = 0; i < 5; i++) {
float dist = distance(st, point[i]);
if ( dist < m_dist ) {
// Keep the closer distance
m_dist = dist;
// Kepp the position of the closer point
m_point = point[i];
}
}
// Add distance field to closest point center
color += m_dist*2.;
// tint acording the closest point position
color.rg = m_point;
// Show isolines
color -= abs(sin(80.0*m_dist))*0.07;
// Draw point center
color += 1.-step(.02, m_dist);
gl_FragColor = vec4(color,1.0);
}위 예제에서는 마우스 위치에 따라 셀이 움직인다.
또한 셀의 색상도 위치에 따라 변한다.
위치값을 이용해 색을 변화하고 있기 때문이다.
// Steven Worley 접근 방식으로 바꾸기
이제 이를 확장하여 Steven Worley의 논문 접근 방식으로 바꿔보자.
스티븐 월리의 원래 접근 방식은 각 타일에서 여러개의 포인트를 사용한다.
또한 대부분의 타일에서 두 개 이상의 피처 포인트를 사용한다는 점에 유의하라.
그가 C로 구현한 소프트웨어에서는 조기 종료를 사용해 루프 속도를 높이고 있다.
하지만 GLSL에서의 루프는 가변 반복 횟수를 허용하지 않으므로 타일당 하나의 피처 포인트를 사용하는 것이 좋다.

vec2 random2( vec2 p ) {
return fract(sin(vec2(dot(p,vec2(127.1,311.7)),dot(p,vec2(269.5,183.3))))*43758.5453);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(.0);
// Scale
st *= 5.;
// Tile the space
vec2 i_st = floor(st);
vec2 f_st = fract(st);
float m_dist = 10.; // minimum distance
vec2 m_point; // minimum point
for (int j=-1; j<=1; j++ ) {
for (int i=-1; i<=1; i++ ) {
vec2 neighbor = vec2(float(i),float(j));
vec2 point = random2(i_st + neighbor);
point = 0.5 + 0.5*sin(u_time + 6.2831*point);
vec2 diff = neighbor + point - f_st;
float dist = length(diff);
if( dist < m_dist ) {
m_dist = dist;
m_point = point;
}
}
}
// Assign a color using the closest point position
color += dot(m_point,vec2(.3,.6));
// Add distance field to closest point center
// color.g = m_dist;
// Show isolines
color -= abs(sin(40.0*m_dist))*0.07;
// Draw cell center
color += 1.-step(.05, m_dist);
// Draw grid
color.r += step(.98, f_st.x) + step(.98, f_st.y);
gl_FragColor = vec4(color,1.0);
}
Improving Voronoi
2011년에 스테판 구스타프슨은 스티븐 월리의 알고리즘을 3x3 대신,
2x2 매트릭스를 반복하는 방식으로 GPU에 최적화했다.
이렇게 하면 연산량이 크게 줄어들지만, 타일 사이의 가장자리에 아티팩트가 발생한다.
다음 예시를 보자.

// Permutation polynomial: (34x^2 + x) mod 289
vec3 permute(vec3 x) {
return mod((34.0 * x + 1.0) * x, 289.0);
}
// Cellular noise, returning F1 and F2 in a vec2.
// Standard 3x3 search window for good F1 and F2 values
vec2 cellular(vec2 P) {
#define K 0.142857142857 // 1/7
#define Ko 0.428571428571 // 3/7
#define jitter 1.0 // Less gives more regular pattern
vec2 Pi = mod(floor(P), 289.0);
vec2 Pf = fract(P);
vec3 oi = vec3(-1.0, 0.0, 1.0);
vec3 of = vec3(-0.5, 0.5, 1.5);
vec3 px = permute(Pi.x + oi);
vec3 p = permute(px.x + Pi.y + oi); // p11, p12, p13
vec3 ox = fract(p*K) - Ko;
vec3 oy = mod(floor(p*K),7.0)*K - Ko;
vec3 dx = Pf.x + 0.5 + jitter*ox;
vec3 dy = Pf.y - of + jitter*oy;
vec3 d1 = dx * dx + dy * dy; // d11, d12 and d13, squared
p = permute(px.y + Pi.y + oi); // p21, p22, p23
ox = fract(p*K) - Ko;
oy = mod(floor(p*K),7.0)*K - Ko;
dx = Pf.x - 0.5 + jitter*ox;
dy = Pf.y - of + jitter*oy;
vec3 d2 = dx * dx + dy * dy; // d21, d22 and d23, squared
p = permute(px.z + Pi.y + oi); // p31, p32, p33
ox = fract(p*K) - Ko;
oy = mod(floor(p*K),7.0)*K - Ko;
dx = Pf.x - 1.5 + jitter*ox;
dy = Pf.y - of + jitter*oy;
vec3 d3 = dx * dx + dy * dy; // d31, d32 and d33, squared
// Sort out the two smallest distances (F1, F2)
vec3 d1a = min(d1, d2);
d2 = max(d1, d2); // Swap to keep candidates for F2
d2 = min(d2, d3); // neither F1 nor F2 are now in d3
d1 = min(d1a, d2); // F1 is now in d1
d2 = max(d1a, d2); // Swap to keep candidates for F2
d1.xy = (d1.x < d1.y) ? d1.xy : d1.yx; // Swap if smaller
d1.xz = (d1.x < d1.z) ? d1.xz : d1.zx; // F1 is in d1.x
d1.yz = min(d1.yz, d2.yz); // F2 is now not in d2.yz
d1.y = min(d1.y, d1.z); // nor in d1.z
d1.y = min(d1.y, d2.x); // F2 is in d1.y, we're done.
return sqrt(d1.xy);
}
void main(void) {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st *= 10.;
vec2 F = cellular(st+vec2(u_time,0.));
float facets = 0.1+(F.y-F.x);
float dots = smoothstep(0.05, 0.1, F.x);
float n = facets * dots;
gl_FragColor = vec4(n, n, n, 1.0);
}
2012년 후반에 이니고 퀼레즈는 정확한 보로노이 테두리를 만드는 방법에 대한 글을 썼다.

vec2 random2( vec2 p ) {
return fract(sin(vec2(dot(p,vec2(127.1,311.7)),dot(p,vec2(269.5,183.3))))*43758.5453);
}
vec3 voronoi( in vec2 x ) {
vec2 n = floor(x);
vec2 f = fract(x);
// first pass: regular voronoi
vec2 mg, mr;
float md = 8.0;
for (int j= -1; j <= 1; j++) {
for (int i= -1; i <= 1; i++) {
vec2 g = vec2(float(i),float(j));
vec2 o = random2( n + g );
o = 0.5 + 0.5*sin( u_time + 6.2831*o );
vec2 r = g + o - f;
float d = dot(r,r);
if( d<md ) {
md = d;
mr = r;
mg = g;
}
}
}
// second pass: distance to borders
md = 8.0;
for (int j= -2; j <= 2; j++) {
for (int i= -2; i <= 2; i++) {
vec2 g = mg + vec2(float(i),float(j));
vec2 o = random2( n + g );
o = 0.5 + 0.5*sin( u_time + 6.2831*o );
vec2 r = g + o - f;
if ( dot(mr-r,mr-r)>0.00001 ) {
md = min(md, dot( 0.5*(mr+r), normalize(r-mr) ));
}
}
}
return vec3(md, mr);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(0.);
// Scale
st *= 3.;
vec3 c = voronoi(st);
// isolines
color = c.x*(0.5 + 0.5*sin(64.0*c.x))*vec3(1.0);
// borders
color = mix( vec3(1.0), color, smoothstep( 0.01, 0.02, c.x ) );
// feature points
float dd = length( c.yz );
color += vec3(1.)*(1.0-smoothstep( 0.0, 0.04, dd));
gl_FragColor = vec4(color,1.0);
}
이니고의 보로노이 연구는 계속 되었다.
2014년에 그는 노이즈와 보로노이를 점진적으로 혼합할 수 있는 기능인 voro-noise에 관한 글을 썼다.
노이즈와 보로노이는 비슷하지만 다른 점이 있다.
그리드가 사용되는 방식이 다르다.
노이즈는 랜덤 값 또는 그라데이션을 보간/평균한다.
하지만 보로노이는 가장 가까운 점까지의 거리를 계산한다.
이제 두 가지는 매우 다른 연산일까? 결합해보자.
아래의 이미지는 보간시 중간값을 넣은 결과를 가져온 것이다.
실제 원문에서는 마우스 위치에 따라 실시간 보간을 할 수 있다.

vec3 hash3( vec2 p ) {
vec3 q = vec3( dot(p,vec2(127.1,311.7)),
dot(p,vec2(269.5,183.3)),
dot(p,vec2(419.2,371.9)) );
return fract(sin(q)*43758.5453);
}
float iqnoise( in vec2 x, float u, float v ) {
vec2 p = floor(x);
vec2 f = fract(x);
float k = 1.0+63.0*pow(1.0-v,4.0);
float va = 0.0;
float wt = 0.0;
for (int j=-2; j<=2; j++) {
for (int i=-2; i<=2; i++) {
vec2 g = vec2(float(i),float(j));
vec3 o = hash3(p + g)*vec3(u,u,1.0);
vec2 r = g - f + o.xy;
float d = dot(r,r);
float ww = pow( 1.0-smoothstep(0.0,1.414,sqrt(d)), k );
va += o.z*ww;
wt += ww;
}
}
return va/wt;
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(0.0);
st *= 10.;
float n = iqnoise(st, u_mouse.x/u_resolution.x, u_mouse.y/u_resolution.y);
gl_FragColor = vec4(vec3(n),1.0);
}그 외에 응용 예제도 알아본다.
이는 원문을 참고하자.
https://thebookofshaders.com/12/?lan=kr
The Book of Shaders
Gentle step-by-step guide through the abstract and complex universe of Fragment Shaders.
thebookofshaders.com
이런 동그란 형태도 만들 수 있다.


'셰이더 (Shader) > The Book of Shaders (완)' 카테고리의 다른 글
| [GLSL] 13 - Fractal Brownian Motion (0) | 2023.05.04 |
|---|---|
| [GLSL] 11 - Noise (0) | 2023.04.26 |
| [GLSL] 10 - Random (0) | 2023.04.25 |
| [GLSL] 9 - Patterns (0) | 2023.04.20 |
| [GLSL] 8 - 2D Matrices (1) | 2023.04.20 |




댓글