
수학은 추상적이고 어렵고 지루하다고 생각할 수 있다.
하지만 훌륭한 쉐이더 TD가 되기 위해서는 꼭 필요하다.
하지만 걱정하지 마라. 인간 계산기가 되지 않아도 된다. 오히려 계산기를 사용하는 것이 많은 도움이 된다.
앞으로 다룰 개념과 이론은 어려울 수 있지만, 우리는 수학자가 아니다.
따라서 이론이 왜 작동하는지나 수학적 증명 등을 걱정할 필요는 없다.
우리가 해야 할 일은 연산과 속성을 배우고 필요할 때 적용하는 것 뿐이다.
몇 가지 연산에 익숙해지려면 연습이 필요할 수 있다. 하지만 풀어내지 못해 좌절하진 마라.
쉐이더 TD로서 일상적으로 사용하는 수학의 양은 많지 않다.
익숙해져야 할 연산과 속성은 매우 제한적이다.
쉐이더 TD로서 가치를 크게 높일 수 있는 수학적 연구들도 많이 있지만, 그것은 더 복잡하며 특정한 경우에만 사용한다.
이 장에서는 일상적으로 다룰 수학을 다룰 것이다.
Useful Operation
쉐이더 개발에서 사용하는 대부분의 수학은 0에서 1 사이의 범위 내에 있는 숫자를 다룬다.
때로는 -1에서 1까지 확장되기도 한다.
텍스처 및 객체의 매개변수 좌표가 일반적으로 이 범위에 해당한다.
대부분의 색상과 노이즈 필드도 동일한 범위에 해당하기 때문에 중요하다.
이러한 값을 조작하여 필요한 값을 얻는 것은 중요하다.
이는 우리가 끊임없이 사용할 연산이다. 꼭 기억해야 한다.
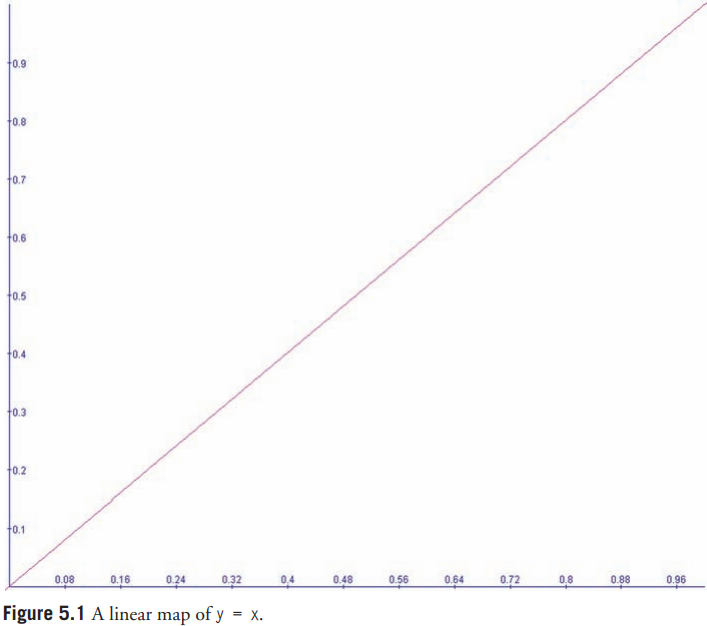
그림 5.1은 y = x의 그래프를 보여준다.
0에서 1까지의 선형 함수를 나타내고 있다.
Inverting a Value
다뤄야하는 값(앞으로는 이 값을 x로 지칭함)이 0에서 1 사이의 범위 내에 있다면,
단순히 값을 1에서 빼는 것으로 반전시킬 수 있다.
이 때 연산은 y = 1 - x; 이다.
왜냐하면 뺄셈은 교환법칙이 없기 때문이다.
즉, y = x - 1;을 입력하면 전혀 다른 결과가 나온다.
만약 x가 -1에서 1 사이의 범위 내에 있다면, 반전을 위한 해결책은 x에 -1을 곱하는 것이다.
예를 들어, y = -1 * x;와 같이 곱해주면 된다.
이 경우 곱셈을 하기 때문에 연산의 순서는 중요하지 않다.
따라서 y = x * -1;와 같이 입력할 수도 있다.
반전을 위한 다른 방법은 부호 반전 연산자(negate operator)를 사용하는 것이다.
이 연산자는 값 앞에 마이너스 기호(-)를 붙여서 사용한다.
예를 들어, -x와 같이 사용한다.
이 연산자는 값을 -1로 곱하는 것과 동일한 효과를 가진다.
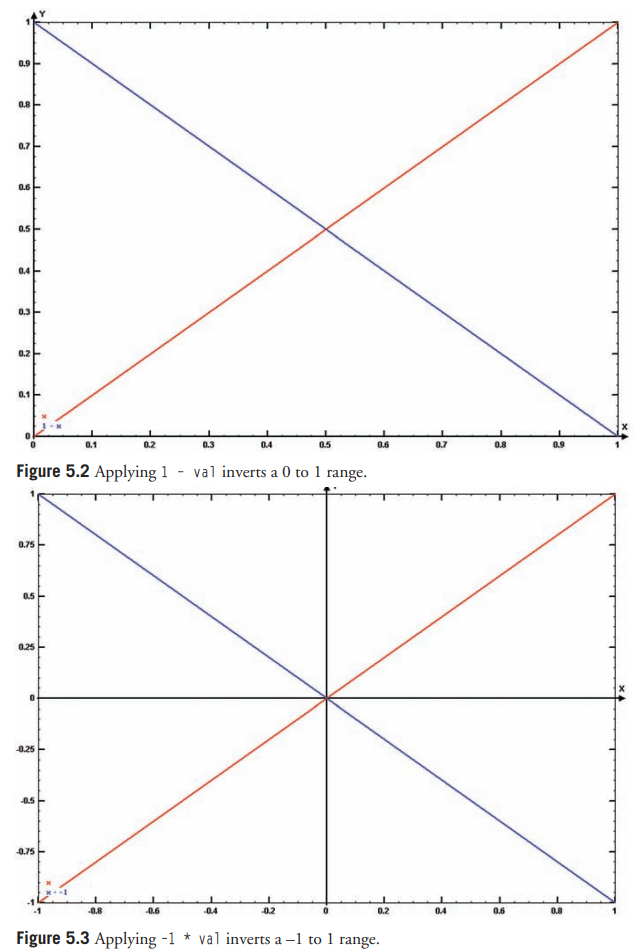
그림 5.2와 5.3은 이러한 반전 방법이 왜 동작하는지에 대한 시각적인 설명이다.
Signing a Value
가끔씩 0에서 1 사이의 범위를 -1에서 1로 바꿔야 할 필요가 있다.
이 작업은 Signing(부호화)이라고 한다.
0에서 1 사이 값을 Signing 하려면, 2를 곱하고 1을 빼면 된다.
즉, y = (2 * x) - 1; 와 같이 계산한다.
Signing은 노이즈 값을 다룰 때 매우 유용하다.
noise() 함수는 보통 0.5 근처의 값을 반환한다.
이 때, 노이즈 값이 -0.5에서 0.5 사이의 값을 평균으로 가져야 하는 경우가 있다.
이런 경우에는 노이즈 값을 Signing 하면 된다.
Figure 5.4는 0에서 1까지의 값을 Signing 하여 -1에서 1로 바꾸는 그래프를 보여준다.

Divide Value by 1
셰이더를 개발하면서 때로는 셰이더 매개변수로는 전혀 적절하지 않은 값을 사용해야 할 때가 있다.
이러한 예로는 텍스처를 확대/축소하는 경우이다.
텍스처 공간 (s, t)은 일반적으로 0에서 1까지의 범위 내에 있다.
텍스처를 확대/축소하기 위해서는, 셰이더 입력 txscale을 가져와 s 또는 t 값으로 나눈다.
하지만 이 방식은 문제가 있다.
텍스처 좌표가 0일 때, 오류가 발생한다.
0으로 값을 나눌 수 없기 때문이다.
다음 코드는 대개 렌더링 오류를 생성한다.
float ss = s/txscale;
float tt = t/txscale;
이 문제를 해결하기 위해, 우리는 접근 방식을 반대로 하고 0으로 나누는 것을 피하기 위한 논리를 추가해야한다.
이를 위해 s와 t 값을 1/txscale로 곱할 것이다.
이렇게 하면 텍스처 좌표를 축소하고 텍스처를 확대할 수 있다.
0으로 나누는 것을 방지하기 위해 매우 작은 수보다 작은 값은 없도록 max()를 사용할 것이다.
다음은 수정된 코드이다.
float scaler = max(1/txscale,0.000001);
float ss = s * scaler;
float tt = t * scaler;
Parametrizing a Value
0~1 범위의 값을 유용한 값으로 변환하는 작업을, 리매핑 또는 매개변수화(parameterizing)라고 한다.
이 기법의 사용 예시 중 하나는 phong() 조명 호출에 전달되는 광택 값(specular value)을 조작하려는 경우이다.
예를 들어 20에서 45 사이의 값을 전달하면 좋은 결과가 나타난다고 가정해보자.
이를 어떻게 구현할 수 있을까?
이 문제를 해결하기 위해 사용자 입력(x)에 대해 값의 범위를 지정하고,
최소값(20)을 빼서 최대값(40)과의 차를 구한 다음, 사용자 입력값과 곱하고 최소값을 다시 더한다.
이를 통해 사용자는 0에서 1 사이의 값을 사용하지만 내부적으로는 20과 45 사이의 선형 보간으로 처리된다.
전처리 매크로를 정의하면 값의 정규화 프로세스를 단순화할 수도 있다.
매크로와 간단한 사용 예를 보자.
#define parametrizeVal(x,lo,hi) lo + x * (hi - lo)
float specval = parametrizeVal(specParam,20,45);
float phongValue = phong(N,I,specval);
bias() and gain()
매우 유용한 함수들을 알아보자.
이 함수들은 Ken Perlin에 의해 개발되었으며, 필수적인 함수이다.
이 두 함수는 기본값이 0.5이어야 하며, 이 경우 입력 값에 영향을 미치지 않는다.
bias() 함수는 가중치 조절기처럼 동작한다.
0에서 1 사이의 범위 중 어느 부분이 더 큰 가중치를 가지는지 제어할 수 있다.
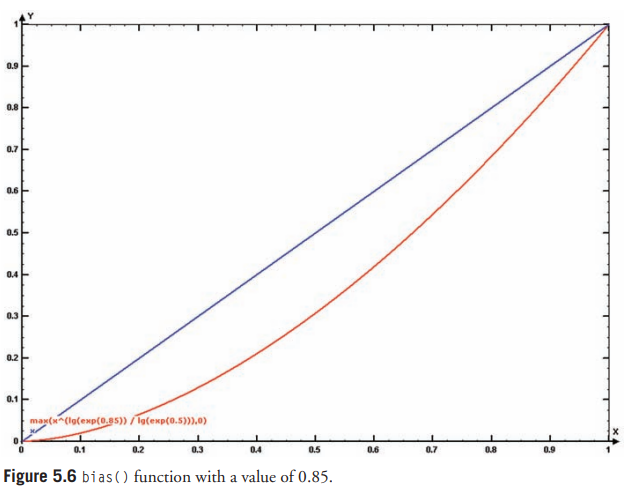
아래는 bias() 함수 코드이다.
이하 그림 2개는 0.25 및 0.85 값을 적용한 결과도 보여준다.
float bias(varying float val,b){
return (b > 0) ? pow(val,log(b) / log(0.5)): 0;
}
gain() 함수는 매우 다른 동작을 한다.
0, 0.5, 1의 값을 변경하지 않는다.
첫 번째 세그먼트(0에서 0.5까지)와 두 번째 세그먼트(0.5에서 1까지)의 값을 조절한다.
내부적으로는 첫 번째 및 두 번째 세그먼트에 대해 적용된 두 개의 bias() 연산으로 계산된다.
gain() 함수의 시각적 결과는 대비를 증가 또는 감소시키는 것이다.
아래 그림은 0.25 및 0.85 일때, gain() 함수의 그래프를 나타낸다.
float gain(float val,g){
return 0.5 * ((val < 0.5) ? bias(2 * val,1 - g) :
(2 - bias(2 - 2 * val,1 - g)));
}
gamma()
gamma() 함수는 bias()와 비슷한 함수이다.
이 함수는 감마 보정에서 사용되며, 애니메이션 및 VFX 산업에서 이미지를 조작하는 표준 방법이다.
색상 수학 및 색상 공간으로 이동할 때 gamma 보정에 대한 보다 깊은 논의를 할 것이다.
gamma() 함수는 매우 간단하다.
y = pow(x,1/gammavalue)로 정의된다.
이 연산은 float 값을 반환한다.
따라서 색상을 gamma 보정하려면 색상의 모든 채널에 gamma() 함수를 적용해야한다.

#define gamma(x,value) pow(x,1/value)
color col1 = color (0.5,0.5,0.5);
color gammacol1 = color(gamma(comp(col1,0),gammaval),
gamma(comp(col1,1),gammaval),
gamma(comp(col1,2),gammaval));
PRMan 13.0부터는 새로운 색상 배열 표기법을 사용할 수도 있다.
color col1 = color (0.5,0.5,0.5);
color gammacol1 = color(gamma(col1[0],gammaval),
gamma(col1[1],gammaval),
gamma(col1[2],gammaval));
그림 5.9와 5.10은, 각각 0.4545와 2.2에서 gamma() 함수의 그래프를 보여준다.


compress() and expand()
이 함수들은 0에서 1까지의 값을 조작하여 동적 범위를 조절할 수 있도록 해준다.
이 두 작업의 출력은 텍스처의 대비를 증가시키거나 감소시키는 것과 유사해 보일 수 있다.
그러나 compress()와 expand()는 실제로 텍스처의 범위를 변경한다.
반면, gain()에서는 0은 0 그대로이고, 1은 1 그대로이다.
compress() 함수는 텍스처의 동적 범위를 더욱 좁게 만들어주며, 다음과 같은 구문을 따른다.
compress(value,lo,hi)compress() 함수는 lo가 최소값이고, hi가 최대값으로 리매핑되는 값을 나타낸다.
compress()는 lo와 hi 값을 값 그래프에서 낮은 위치로 밀어내어 리매핑한다.
compress(s,0,2)로 작성시, 1의 값을 2로 리매핑하고 0.5는 1로 리매핑한다.
0은 변경하지 않는다.
compress(s,0.5,1)로 작성시, 0의 값을 0.5로 리매핑하고 0.5의 값을 0.75로 리매핑한다.
1은 변경하지 않는다.
Figure 5.11은 (x,0,2)와 (x,0.25,0.75)에서의 compress()를 보여주는 그래프이다.
Figures 5.12에서 5.14는 compress()를 사용한 결과를 보여준다.
float compress(float x, float lo, float hi) {
return (hi-lo) * x + lo;
}


expand() 함수는 compress()의 반대로 작동한다.
이 함수는 값을 높은 위치로 밀어올려 값을 리매핑한다.
expand(s,0.5,1)로 작성시, 0과 1은 그대로 둔다.
0.5는 0으로 리매핑한다.
0을 0.5 위치로 올리고, 0.5를 0으로 리매핑한다.
expand(s,0,2)로 작성시, 0은 그대로 둔다.
1은 0.5로 리매핑한다.
1을 2 위치로 올린다.
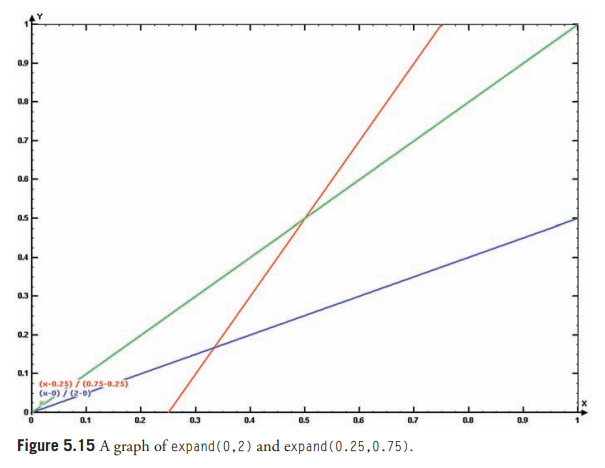
Figure 5.15는 expand(0,2) 및 expand(0.25,0.75)의 그래프를 보여준다.
Figures 5.16 및 5.17은 s 좌표에 expand()를 적용한 결과를 보여준다.
float expand(float x, float lo, float hi) {
float retval = 0;
if (lo == hi)
retval = x < lo ? 0 : 1;
else
retval = (x-lo) / (hi-lo);
return retval;
}

remap()
실수 연산이다.
x의 최소 및 최대값(a1과 b1)을 가져와서,
새로운 최소 및 최대값(a2와 b2)으로 선형적으로 만든다.
remap(x,0,1,1,0)을 사용하면 x의 값을 반전한다.
함수를 remap(x,0,1,0.25,0.75)로 설정하면,
그림 5.18에 나와있는 대로 0.25에서 0.75로 리매핑한다.

'셰이더 (Shader) > The Renderman Shading Language Guide' 카테고리의 다른 글
| [RSL] Part2 : Divide and Conquer (162p ~ 179p) (0) | 2023.08.19 |
|---|---|
| [RSL] Part2 : Shader Design Methodology (158p ~ 161p) (0) | 2023.08.19 |
| [RSL] Part2 : Color Math (134p ~ 155p) (0) | 2023.05.30 |
| [RSL] Part2 : Trigonometry, Vector Math (123p ~ 134p) (0) | 2023.05.16 |
| [RSL] Part1 : Your First Shader (66p ~ 91p) (1) | 2023.05.08 |




댓글